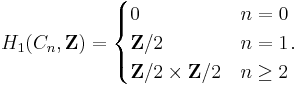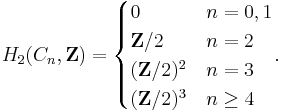Hyperoctahedral group


The C2 group has order 8 as shown on this circle
The C3 (Oh) group has order 48 as shown by these spherical triangle reflection domains.

In mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. Groups of this type are identified by a parameter n, the dimension of the hypercube.

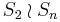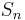As a Coxeter group it is of type Bn = Cn, and as a Weyl group it is associated to the orthogonal groups in odd dimensions. As a wreath product it is S_2 \wr S_n where S_n is the symmetric group of degree n. As a permutation group, the group is the signed symmetric group of permutations π either of the set { −n, −n + 1, ..., −1, 1, 2, ..., n } or of the set { −n, −n + 1, ..., n } such that π(i) = −π(−i) for all i. As a matrix group, it can be described as the group of n×n orthogonal matrices whose entries are all integers. The representation theory of the hyperoctahedral group was described by (Young 1930) according to (Kerber 1971, p. 2).

In three dimensions, the hyperoctahedral group is known as O×S2 where O≅S4 is the octahedral group, and S2 is a symmetric group (equivalently, cyclic group) of order 2. Geometric figures in three dimensions with this symmetry group are said to have octahedral symmetry. In two dimensions, the hyperoctahedral group is known as the dihedral group of order eight, describing the symmetry of a square.

Contents

By dimension

Hyperoctahedral groups can be named as Cn, a bracket notation, or as a Coxeter group graph:

n Symmetry
group		 Cn Coxeter notation Coxeter group
graph		 Symmetry order Structure Related regular and uniform polytopes
2 D4 (*44) C2 [4] 222! = 8 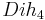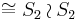Dih_4 \cong S_2 \wr S_2 Square, octagon
3 Oh (*432) C3 [4,3] 233! = 48 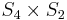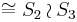S_4 \times S_2 \cong S_2 \wr S_3 Cube, octahedron, truncated cube, truncated octahedron, cuboctahedron, rhombicuboctahedron ...
4   C4 [4,3,3] 244! = 384 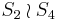S_2 \wr S_4 Tesseract, 16-cell, 24-cell, truncated tesseract, truncated 16-cell, rectified tesseract, rectified 16-cell, cantellated tesseract, runcinated tesseract, ...
5   C5 [4,3,3,3] 255! = 3840 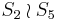S_2 \wr S_5 Penteract, pentacross, truncated penteract, truncated pentacross, rectified penteract, rectified pentacross, ...
6   C6 [4,34] 266! = 46080 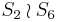S_2 \wr S_6
...
n   Cn [4,3n-2] ... 2nn! 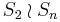S_2 \wr S_n

Subgroups

There is a notable index two subgroup, corresponding to the Coxeter group Dn and the symmetries of the demihypercube. Viewed as a wreath product, there are two natural maps from the hyperoctahedral group to the cyclic group of order 2: one map coming from "multiply the signs of all the elements" (in the n copies of 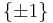\{\pm 1\}), and one map coming from the parity of the permutation. Multiplying these together yields a third map 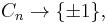C_n \to \{\pm 1\}, and the kernel of this map is the Coxeter group 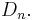D_n. In terms of signed permutations, thought of as matrices, this third map is simply the determinant, while the first two correspond to "multiplying the non-zero entries" and "parity of the underlying (unsigned) permutation", which are not generally meaningful for matrices, but are in the case due to the coincidence with a wreath product.

The kernels of these three maps are all three index two subgroups of the hyperoctahedral group, as discussed in H1: Abelianization below, and their intersection is the derived subgroup, of index 4 (quotient the Klein 4-group), which corresponds to the rotational symmetries of the demihypercube.

In the other direction, the center is the subgroup of scalar matrices, {±1}; geometrically, quotienting out by this corresponds to passing to the projective orthogonal group.

In dimension 2 these groups completely describe the hyperoctahedral group, which is the dihedral group Dih4 of order 8, and is an extension 2.V (of the 4-group by a cyclic group of order 2). In general, passing to the subquotient (derived subgroup, mod center) is the symmetry group of the projective demihypercube.

Homology

The group homology of the hyperoctahedral group is similar to that of the symmetric group, and exhibits stabilization, in the sense of stable homotopy theory.

H1: abelianization

The first homology group, which agrees with the abelianization, stabilizes at the Klein four-group, and is given by:

H_1(C_n, \mathbf{Z}) = \begin{cases} 0 & n = 0\\ \mathbf{Z}/2 & n = 1\\ \mathbf{Z}/2 \times \mathbf{Z}/2 & n \geq 2 \end{cases}.

This is easily seen directly: the 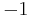-1 elements are order 2 (which is non-empty for 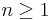n\geq 1), and all conjugate, as are the transpositions in 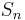S_n (which is non-empty for 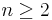n\geq 2), and these are two separate classes. These elements generate the group, so the only non-trivial abelianizations are to 2-groups, and either of these classes can be sent independently to 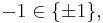-1 \in \{\pm 1\}, as they are two separate classes. The maps are explicitly given as "the product of the signs of all the elements" (in the n copies of 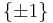\{\pm 1\}), and the sign of the permutation. Multiplying these together yields a third non-trivial map (the determinant of the matrix, which sends both these classes to 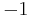-1), and together with the trivial map these form the 4-group.

H2: Schur multipliers

The second homology groups, known classically as the Schur multipliers, were computed in (Ihara & Yokonuma 1965).

They are:

H_2(C_n,\mathbf{Z}) = \begin{cases} 0 & n = 0, 1\\ \mathbf{Z}/2 & n = 2\\ (\mathbf{Z}/2)^2 & n = 3\\ (\mathbf{Z}/2)^3 & n \geq 4 \end{cases}.

References